Module 2, Practical 7
In this practical we will keep working with data structures. In particular, we will see a special data structure called tree.
Trees
Trees are data structures composed of two types of elements: nodes and edges.
Nodes represent objects and edges represent relationships among two nodes.
The node at the top level of the tree is called the root, and is connected to one or more other nodes.
If the root is connected to another node by means of one edge, then it is said to be the parent of the node (and that node is the child of the root).
Any node can be parent of one or more other nodes, but all nodes have only one parent.
The root is the only exception as it does not have any parent.
Finally, some nodes do not have children and they are called leaves.
An example of tree:
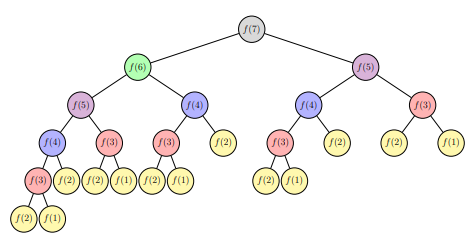
As seen in the lecture, trees can be defined recursively in the following way: a tree is a root and zero or more subtrees, each of which is also a tree. The root of each subtree is connected to the root of the parent tree by an edge.
Graphically:
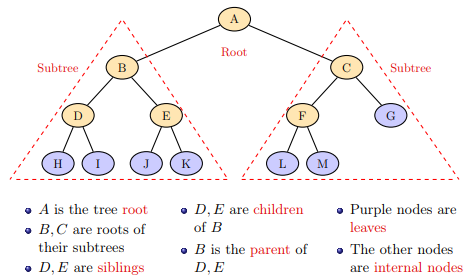
Some properties of nodes and trees are:
The depth of a node N: the length of the path connecting the root to N counted as number of edges in the path.
The level (n) of a tree: set of nodes at the same depth (n).
Height : is the maximum depth of all leaves.
Width : the maximum number of nodes in each level.
The following tree:
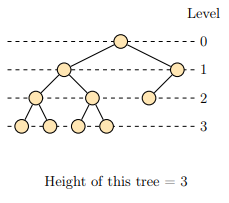
has four levels (0, 1, 2, 3), height equal to 3 and width equal to 4.
ADT: Binary Tree
Binary trees are trees where each node has at most two children: the right child and the left child.
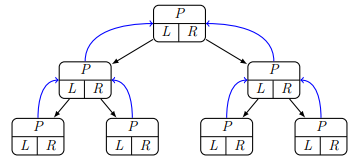
The specifications of the binary tree ADT (from the lecture):
When implementing a tree we could (similarly to what we did with linked lists) define a node object, and then a tree object that stores nodes, but we will use the more compact way which is to use the recursive definition of a tree.
Example: Let’s implement a binary tree using the recursive definition:
>a binary tree is a root –with a value – connected to two subtrees, respectively the right and left subtree.
[1]:
class BinaryTree:
def __init__(self, value):
self.__data = value
self.__right = None
self.__left = None
self.__parent = None
def getValue(self):
return self.__data
def setValue(self, newValue):
self.__data = newValue
def getParent(self):
return self.__parent
def setParent(self, tree):
self.__parent = tree
def getRight(self):
return self.__right
def getLeft(self):
return self.__left
def insertRight(self, tree):
if self.__right == None:
self.__right = tree
tree.setParent(self)
def insertLeft(self, tree):
if self.__left == None:
self.__left = tree
tree.setParent(self)
def deleteRight(self):
self.__right = None
def deleteLeft(self):
self.__left = None
def printTree(root):
cur = root
#each element is a node and a depth
#depth is used to format prints (with tabs)
nodes = [(cur,0)]
tabs = ""
lev = 0
while len(nodes) >0:
cur, lev = nodes.pop(-1)
#print("{}{}".format("\t"*lev, cur.getValue()))
if cur.getRight() != None:
print ("{}{} (r)-> {}".format("\t"*lev,
cur.getValue(),
cur.getRight().getValue()))
nodes.append((cur.getRight(), lev+1))
if cur.getLeft() != None:
print ("{}{} (l)-> {}".format("\t"*lev,
cur.getValue(),
cur.getLeft().getValue()))
nodes.append((cur.getLeft(), lev+1))
if __name__ == "__main__":
BT = BinaryTree("Root")
bt1 = BinaryTree(1)
bt2 = BinaryTree(2)
bt3 = BinaryTree(3)
bt4 = BinaryTree(4)
bt5 = BinaryTree(5)
bt6 = BinaryTree(6)
bt5a = BinaryTree("5a")
bt5b = BinaryTree("5b")
bt5c = BinaryTree("5c")
BT.insertLeft(bt1)
BT.insertRight(bt2)
bt2.insertLeft(bt3)
bt3.insertLeft(bt4)
bt3.insertRight(bt5)
bt2.insertRight(bt6)
bt1.insertRight(bt5b)
bt1.insertLeft(bt5a)
bt5b.insertRight(bt5c)
printTree(BT)
print("\nDelete right branch of 2")
bt2.deleteRight()
printTree(BT)
print("\nInsert left branch of 5")
newN = BinaryTree("child of 5")
bt5.insertLeft(newN)
printTree(BT)
Root (r)-> 2
Root (l)-> 1
1 (r)-> 5b
1 (l)-> 5a
5b (r)-> 5c
2 (r)-> 6
2 (l)-> 3
3 (r)-> 5
3 (l)-> 4
Delete right branch of 2
Root (r)-> 2
Root (l)-> 1
1 (r)-> 5b
1 (l)-> 5a
5b (r)-> 5c
2 (l)-> 3
3 (r)-> 5
3 (l)-> 4
Insert left branch of 5
Root (r)-> 2
Root (l)-> 1
1 (r)-> 5b
1 (l)-> 5a
5b (r)-> 5c
2 (l)-> 3
3 (r)-> 5
3 (l)-> 4
5 (l)-> child of 5
Download the complete source file: BinaryTree.py
Note that in the code above, to delete the right or left subtree you just set the pointer to null. This destroys the whole subtree (more clever things can be done in some cases, especially with generic trees).
Exercise
Modify the BinaryTree class adding a
depthparameter counting, for each subtree, its depth (i.e. distance from the root of the tree). Note that you have to update properly the depth when inserting a new node. Add agetDepthandsetDepthmethod too.
Test the code printing the depth of all the nodes of the binary graph:
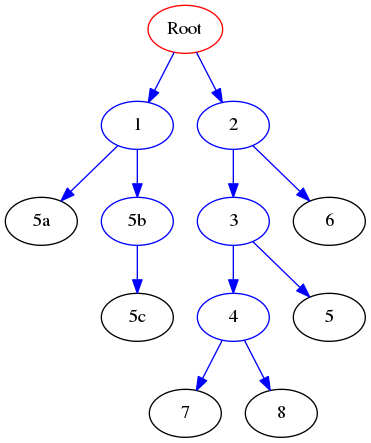
that can be created with:
BT = BinaryTree("Root")
bt1 = BinaryTree(1)
bt2 = BinaryTree(2)
bt3 = BinaryTree(3)
bt4 = BinaryTree(4)
bt5 = BinaryTree(5)
bt6 = BinaryTree(6)
bt5a = BinaryTree("5a")
bt5b = BinaryTree("5b")
bt5c = BinaryTree("5c")
bt7 = BinaryTree(7)
bt8 = BinaryTree(8)
BT.insertLeft(bt1)
BT.insertRight(bt2)
bt2.insertLeft(bt3)
bt3.insertLeft(bt4)
bt3.insertRight(bt5)
bt2.insertRight(bt6)
bt1.insertRight(bt5b)
bt1.insertLeft(bt5a)
bt5b.insertRight(bt5c)
bt4.insertRight(bt7)
bt4.insertLeft(bt8)
Show/Hide Solution
[ ]:
class BinaryTree:
def __init__(self, value):
self.__data = value
self.__right = None
self.__left = None
self.__parent = None
self.__depth = 0 # new param
def getValue(self):
return self.__data
def setValue(self, newval):
self.__data = newval
def getParent(self):
return self.__parent
def setParent(self, tree):
self.__parent = tree
def getRight(self):
return self.__right
def getLeft(self):
return self.__left
# new method
def getDepth(self):
return self.__depth
# new method
def setDepth(self, newdepth):
self.__depth = newdepth
def insertRight(self, tree):
if self.__right == None:
self.__right = tree
tree.setParent(self)
tree.setDepth(self.getDepth() + 1)
def insertLeft(self, tree):
if self.__left == None:
self.__left = tree
tree.setParent(self)
tree.setDepth(self.getDepth() + 1)
def deleteRight(self):
self.__right = None
def deleteLeft(self):
self.__left = None
def printTree(root):
cur = root
#each element is a node and a depth
#depth is used to format prints (with tabs)
nodes = [(cur,0)]
tabs = ""
lev = 0
while len(nodes) >0:
cur, lev = nodes.pop(-1)
#print("{}{}".format("\t"*lev, cur.getValue()))
if cur.getRight() != None:
print ("{}{} (r)-> {}".format("\t"*lev,
cur.getValue(),
cur.getRight().getValue()))
nodes.append((cur.getRight(), lev+1))
if cur.getLeft() != None:
print ("{}{} (l)-> {}".format("\t"*lev,
cur.getValue(),
cur.getLeft().getValue()))
nodes.append((cur.getLeft(), lev+1))
if __name__ == "__main__":
BT = BinaryTree("Root")
bt1 = BinaryTree(1)
bt2 = BinaryTree(2)
bt3 = BinaryTree(3)
bt4 = BinaryTree(4)
bt5 = BinaryTree(5)
bt6 = BinaryTree(6)
bt5a = BinaryTree("5a")
bt5b = BinaryTree("5b")
bt5c = BinaryTree("5c")
bt7 = BinaryTree(7)
bt8 = BinaryTree(8)
BT.insertLeft(bt1)
BT.insertRight(bt2)
bt2.insertLeft(bt3)
bt3.insertLeft(bt4)
bt3.insertRight(bt5)
bt2.insertRight(bt6)
bt1.insertRight(bt5b)
bt1.insertLeft(bt5a)
bt5b.insertRight(bt5c)
bt4.insertRight(bt7)
bt4.insertLeft(bt8)
nodeList = [BT,bt1,bt2,bt3,bt4, bt5, bt5a, bt5b,
bt5c, bt6, bt7, bt8]
for node in nodeList:
if node != None:
print("Node {} has depth: {}".format(node.getValue(),
node.getDepth()))
Node Root has depth: 0
Node 1 has depth: 1
Node 2 has depth: 1
Node 3 has depth: 2
Node 4 has depth: 3
Node 5 has depth: 3
Node 5a has depth: 2
Node 5b has depth: 2
Node 5c has depth: 3
Node 6 has depth: 2
Node 7 has depth: 4
Node 8 has depth: 4
Download the complete source file: BinaryTree2.py
Tree visit
Now we can see how to perform some visits of the trees, that is going through the nodes following the connections.
In particular, there are two different types of visits: depth first and breadth first search.
Binary Tree visits: DFS
Given a tree T, depth first search (DFS) visits all the subtrees of T going as deep as it can before going back and down another branch until all the tree is visited.
DFS requires a stack and can be implemented recursively. What we do with the root during the visit defines 3 different types of visits:
the root is visited before the visiting the subtree : pre-order;
the root is visited after the left subtree but before the right subtree : in-order;
the root is visited after the left and right subtrees : post-order.
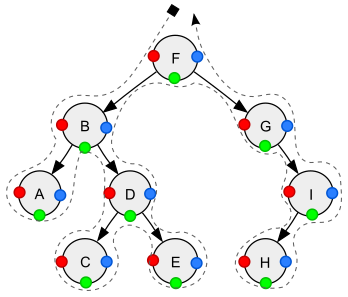
Depth-first traversal (dotted path) of a binary tree:
Pre-order (node visited at position red): F, B, A, D, C, E, G, I, H;
In-order (node visited at position green): A, B, C, D, E, F, G, H, I;
Post-order (node visited at position blue): A, C, E, D, B, H, I, G, F.
Example: Let’s implement the three versions of DFS and apply them to the binary tree seen above.
[3]:
class BinaryTree:
def __init__(self, value):
self.__data = value
self.__right = None
self.__left = None
self.__parent = None
def getValue(self):
return self.__data
def setValue(self, newValue):
self.__data = newValue
def getParent(self):
return self.__parent
def setParent(self, tree):
self.__parent = tree
def getRight(self):
return self.__right
def getLeft(self):
return self.__left
def insertRight(self, tree):
if self.__right == None:
self.__right = tree
tree.setParent(self)
def insertLeft(self, tree):
if self.__left == None:
self.__left = tree
tree.setParent(self)
def deleteRight(self):
self.__right = None
def deleteLeft(self):
self.__left = None
def preOrderDFS(self):
if self != None:
r = self.getRight()
l = self.getLeft()
print(self.getValue()) # print before recursive calls!
if l != None:
l.preOrderDFS()
if r != None:
r.preOrderDFS()
def inOrderDFS(self):
if self != None:
r = self.getRight()
l = self.getLeft()
if l != None:
l.inOrderDFS()
print(self.getValue()) # print in the between the recursive calls!
if r != None:
r.inOrderDFS()
def postOrderDFS(self):
if self != None:
r = self.getRight()
l = self.getLeft()
if l != None:
l.postOrderDFS()
if r != None:
r.postOrderDFS()
print(self.getValue()) # print after the recursive calls!
def printTree(root):
cur = root
#each element is a node and a depth
#depth is used to format prints (with tabs)
nodes = [(cur,0)]
tabs = ""
lev = 0
while len(nodes) >0:
cur, lev = nodes.pop(-1)
#print("{}{}".format("\t"*lev, cur.getValue()))
if cur.getRight() != None:
print ("{}{} (r)-> {}".format("\t"*lev,
cur.getValue(),
cur.getRight().getValue()))
nodes.append((cur.getRight(), lev+1))
if cur.getLeft() != None:
print ("{}{} (l)-> {}".format("\t"*lev,
cur.getValue(),
cur.getLeft().getValue()))
nodes.append((cur.getLeft(), lev+1))
if __name__ == "__main__":
BT = BinaryTree("Root")
bt1 = BinaryTree(1)
bt2 = BinaryTree(2)
bt3 = BinaryTree(3)
bt4 = BinaryTree(4)
bt5 = BinaryTree(5)
bt6 = BinaryTree(6)
bt5a = BinaryTree("5a")
bt5b = BinaryTree("5b")
bt5c = BinaryTree("5c")
BT.insertLeft(bt1)
BT.insertRight(bt2)
bt2.insertLeft(bt3)
bt3.insertLeft(bt4)
bt3.insertRight(bt5)
bt2.insertRight(bt6)
bt1.insertRight(bt5b)
bt1.insertLeft(bt5a)
bt5b.insertRight(bt5c)
printTree(BT)
print("Pre-order DFS:")
BT.preOrderDFS()
print("\nIn-order DFS:")
BT.inOrderDFS()
print("\nPost-order DFS:")
BT.postOrderDFS()
Root (r)-> 2
Root (l)-> 1
1 (r)-> 5b
1 (l)-> 5a
5b (r)-> 5c
2 (r)-> 6
2 (l)-> 3
3 (r)-> 5
3 (l)-> 4
Pre-order DFS:
Root
1
5a
5b
5c
2
3
4
5
6
In-order DFS:
5a
1
5b
5c
Root
4
3
5
2
6
Post-order DFS:
5a
5c
5b
1
4
5
3
6
2
Root
Download the complete source file: BinaryTreeDFSVisits.py
Compare the results above with the graph:
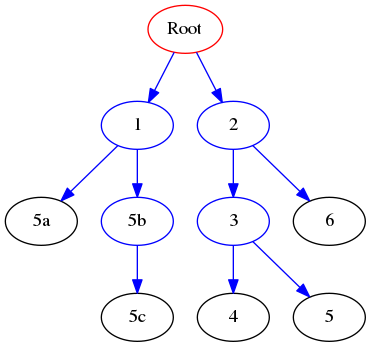
Binary Tree visits: BFS
Breadth first search visits all the higher levels of a tree before going down. Basically, this search goes as wide as it can before going deep.
This visit makes use of a queue: for each tree, it adds the left and right subtrees to the queue and recursively visits them in the order they have been pushed into the queue.
As said, implementations of BFS make use of a FIFO queue. In Python, we can use the efficient deque data structure that is implemented in the collections module (remember to import it first with from collections import deque and use deque.append to add at the end and deque.popleft to remove from the beginning).
Example: Let’s implement a BFS method and apply it to binary tree seen above.
[4]:
from collections import deque
class BinaryTree:
def __init__(self, value):
self.__data = value
self.__right = None
self.__left = None
self.__parent = None
def getValue(self):
return self.__data
def setValue(self, newValue):
self.__data = newValue
def getParent(self):
return self.__parent
def setParent(self, tree):
self.__parent = tree
def getRight(self):
return self.__right
def getLeft(self):
return self.__left
def insertRight(self, tree):
if self.__right == None:
self.__right = tree
tree.setParent(self)
def insertLeft(self, tree):
if self.__left == None:
self.__left = tree
tree.setParent(self)
def deleteRight(self):
self.__right = None
def deleteLeft(self):
self.__left = None
def BFS(self):
if self != None:
level = deque()
level.append(self)
while len(level) > 0:
#print(len(level))
cur = level.popleft()
print(cur.getValue())
r = cur.getRight()
l = cur.getLeft()
if l != None:
#print("from {} Appending: {}".format(cur.getValue(),
# l.getValue()))
level.append(l)
if r != None:
level.append(r)
#print("from {} Appending: {}".format(cur.getValue(),
# r.getValue()))
def printTree(root):
cur = root
#each element is a node and a depth
#depth is used to format prints (with tabs)
nodes = [(cur,0)]
tabs = ""
lev = 0
while len(nodes) >0:
cur, lev = nodes.pop(-1)
#print("{}{}".format("\t"*lev, cur.getValue()))
if cur.getRight() != None:
print ("{}{} (r)-> {}".format("\t"*lev,
cur.getValue(),
cur.getRight().getValue()))
nodes.append((cur.getRight(), lev+1))
if cur.getLeft() != None:
print ("{}{} (l)-> {}".format("\t"*lev,
cur.getValue(),
cur.getLeft().getValue()))
nodes.append((cur.getLeft(), lev+1))
if __name__ == "__main__":
BT = BinaryTree("Root")
bt1 = BinaryTree(1)
bt2 = BinaryTree(2)
bt3 = BinaryTree(3)
bt4 = BinaryTree(4)
bt5 = BinaryTree(5)
bt6 = BinaryTree(6)
bt5a = BinaryTree("5a")
bt5b = BinaryTree("5b")
bt5c = BinaryTree("5c")
BT.insertLeft(bt1)
BT.insertRight(bt2)
bt2.insertLeft(bt3)
bt3.insertLeft(bt4)
bt3.insertRight(bt5)
bt2.insertRight(bt6)
bt1.insertRight(bt5b)
bt1.insertLeft(bt5a)
bt5b.insertRight(bt5c)
printTree(BT)
print("BFS:")
BT.BFS()
Root (r)-> 2
Root (l)-> 1
1 (r)-> 5b
1 (l)-> 5a
5b (r)-> 5c
2 (r)-> 6
2 (l)-> 3
3 (r)-> 5
3 (l)-> 4
BFS:
Root
1
2
5a
5b
3
6
5c
4
5
Download the complete source file: BinaryTreeBFSVisit.py
Compare the results above with the graph:
Exercises
The width of a binary tree T is the largest number of nodes that belong to the same level. The minimal height of a binary tree T is the minimal distance between the root and its closest leaf in its subtree. This distance is counted in number of nodes.
Given the BinaryTree defined above:
Write a function
getWidth(T)that given a tree T, returns the width of T. Hint: get all nodes at each level and count them.Write a function
getMinHeight(T)that given a tree T, returns the minimal height of T (in number of nodes). Hint: stop at first level with a leaf (similar to previous function).Write a function
nodesAtLevel(T,k)that given a binary tree T and an integer k, returns the nodes at level k.
Test the functions with the following binary graph:
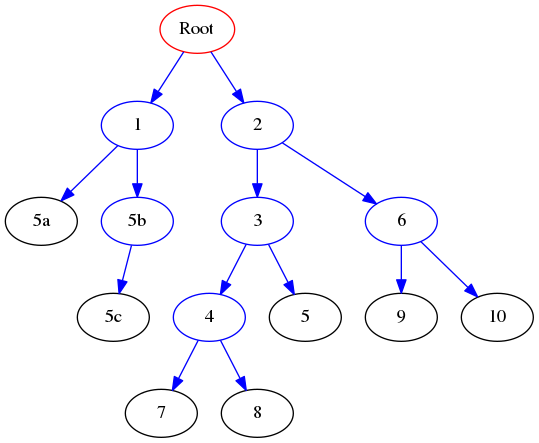
that can be created with:
BT = BinaryTree("Root")
bt1 = BinaryTree(1)
bt2 = BinaryTree(2)
bt3 = BinaryTree(3)
bt4 = BinaryTree(4)
bt5 = BinaryTree(5)
bt6 = BinaryTree(6)
bt5a = BinaryTree("5a")
bt5b = BinaryTree("5b")
bt5c = BinaryTree("5c")
bt7 = BinaryTree(7)
bt8 = BinaryTree(8)
bt9 = BinaryTree(9)
bt10 = BinaryTree(10)
BT.insertLeft(bt1)
BT.insertRight(bt2)
bt2.insertLeft(bt3)
bt3.insertLeft(bt4)
bt3.insertRight(bt5)
bt2.insertRight(bt6)
bt1.insertRight(bt5b)
bt1.insertLeft(bt5a)
bt5b.insertRight(bt5c)
bt4.insertRight(bt7)
bt4.insertLeft(bt8)
bt6.insertRight(bt10)
bt6.insertLeft(bt9)
Show/Hide Solution
[5]:
class BinaryTree:
def __init__(self, value):
self.__data = value
self.__right = None
self.__left = None
self.__parent = None
self.__depth = 0 #new param
# new method
def getDepth(self):
return self.__depth
# new method
def setDepth(self, newdepth):
self.__depth = newdepth
def getValue(self):
return self.__data
def setValue(self, newValue):
self.__data = newValue
def getParent(self):
return self.__parent
def setParent(self, tree):
self.__parent = tree
def getRight(self):
return self.__right
def getLeft(self):
return self.__left
def insertRight(self, tree):
if self.__right == None:
self.__right = tree
tree.setParent(self)
tree.setDepth(self.getDepth() + 1)
def insertLeft(self, tree):
if self.__left == None:
self.__left = tree
tree.setDepth(self.getDepth() + 1)
tree.setParent(self)
def deleteRight(self):
self.__right = None
def deleteLeft(self):
self.__left = None
def getWidth(tree):
"""gets the width of the tree"""
if tree == None:
return 0
level = [tree]
res = 1
while len(level) > 0:
tmp = []
for t in level:
r = t.getRight()
l = t.getLeft()
if r != None:
tmp.append(r)
if l != None:
tmp.append(l)
res = max(res,len(tmp))
level = tmp
return res
def getMinHeight(tree):
"""gets the minimum height of the tree in nodes"""
if tree == None:
return 0
level = [tree]
res = 1
while len(level) > 0:
tmp = []
for t in level:
r = t.getRight()
l = t.getLeft()
if r == None and l == None:
return res
else:
if r != None:
tmp.append(r)
if l != None:
tmp.append(l)
level = tmp
res += 1
return res
def nodesAtLevel(tree,k):
"""returns the nodes at level k"""
if tree == None:
return 0
level = [tree]
cnt = 0
while cnt != k and len(level) > 0:
tmp = []
for t in level:
r = t.getRight()
l = t.getLeft()
if l != None:
tmp.append(l)
if r != None:
tmp.append(r)
level = tmp
cnt += 1
if len(level) == 0:
return None
else:
vals = [x.getValue() for x in level if x != None]
return vals
if __name__ == "__main__":
BT = BinaryTree("Root")
bt1 = BinaryTree(1)
bt2 = BinaryTree(2)
bt3 = BinaryTree(3)
bt4 = BinaryTree(4)
bt5 = BinaryTree(5)
bt6 = BinaryTree(6)
bt5a = BinaryTree("5a")
bt5b = BinaryTree("5b")
bt5c = BinaryTree("5c")
bt7 = BinaryTree(7)
bt8 = BinaryTree(8)
bt9 = BinaryTree(9)
bt10 = BinaryTree(10)
BT.insertLeft(bt1)
BT.insertRight(bt2)
bt2.insertLeft(bt3)
bt3.insertLeft(bt4)
bt3.insertRight(bt5)
bt2.insertRight(bt6)
bt1.insertRight(bt5b)
bt1.insertLeft(bt5a)
bt5b.insertRight(bt5c)
bt4.insertRight(bt7)
bt4.insertLeft(bt8)
bt6.insertRight(bt10)
bt6.insertLeft(bt9)
print("The width of BT is {}".format(getWidth(BT)))
print("The minimum height of BT is {}".format(getMinHeight(BT)))
for i in range(0,6):
print("Nodes at level {}: {}".format(i,nodesAtLevel(BT,i)))
print("The minimum height of BT is {}".format(getMinHeight(BT)))
bt1.deleteLeft()
print("Deleting 5ca")
print("The minimum height of BT is {}".format(getMinHeight(BT)))
bt5d = BinaryTree("5d")
bt5c.insertLeft(bt5d)
print("Adding 5d as left child of 5c")
print("The minimum height of BT is {}".format(getMinHeight(BT)))
The width of BT is 5
The minimum height of BT is 3
Nodes at level 0: ['Root']
Nodes at level 1: [1, 2]
Nodes at level 2: ['5a', '5b', 3, 6]
Nodes at level 3: ['5c', 4, 5, 9, 10]
Nodes at level 4: [8, 7]
Nodes at level 5: None
The minimum height of BT is 3
Deleting 5ca
The minimum height of BT is 4
Adding 5d as left child of 5c
The minimum height of BT is 4
Download the complete source file: BinaryTree3.py
Given the BinaryTree used so far, implement a
getCommonAncestor(n1,n2)method that gets the common ancestor between the two nodes n1 and n2.
For example, considering the graph above:
getCommonAncestor(7,5) = 3
getCommonAncestor(7,10) = 2
getCommonAncestor(8,5b) = Root
Show/Hide Solution
[6]:
class BinaryTree:
def __init__(self, value):
self.__data = value
self.__right = None
self.__left = None
self.__parent = None
self.__depth = 0 #new param
# new method
def getDepth(self):
return self.__depth
# new method
def setDepth(self, newdepth):
self.__depth = newdepth
def getValue(self):
return self.__data
def setValue(self, newValue):
self.__data = newValue
def getParent(self):
return self.__parent
def setParent(self, tree):
self.__parent = tree
def getRight(self):
return self.__right
def getLeft(self):
return self.__left
def insertRight(self, tree):
if self.__right == None:
self.__right = tree
tree.setParent(self)
#line modified
tree.setDepth(self.getDepth() + 1)
def insertLeft(self, tree):
if self.__left == None:
self.__left = tree
#line modified
tree.setDepth(self.getDepth() + 1)
tree.setParent(self)
def deleteRight(self):
self.__right = None
def deleteLeft(self):
self.__left = None
def getCommonAncestor(node1, node2):
if node1 == node2:
return node1
if node1 == None or node2 == None:
return None
n1anc = set()
n1anc.add(node1)
anc = node1.getParent()
while anc != None:
n1anc.add(anc)
anc = anc.getParent()
anc = node2
while anc != None:
if anc in n1anc:
return anc
else:
anc = anc.getParent()
if __name__ == "__main__":
BT = BinaryTree("Root")
bt1 = BinaryTree(1)
bt2 = BinaryTree(2)
bt3 = BinaryTree(3)
bt4 = BinaryTree(4)
bt5 = BinaryTree(5)
bt6 = BinaryTree(6)
bt5a = BinaryTree("5a")
bt5b = BinaryTree("5b")
bt5c = BinaryTree("5c")
bt7 = BinaryTree(7)
bt8 = BinaryTree(8)
bt9 = BinaryTree(9)
bt10 = BinaryTree(10)
BT.insertLeft(bt1)
BT.insertRight(bt2)
bt2.insertLeft(bt3)
bt3.insertLeft(bt4)
bt3.insertRight(bt5)
bt2.insertRight(bt6)
bt1.insertRight(bt5b)
bt1.insertLeft(bt5a)
bt5b.insertRight(bt5c)
bt4.insertRight(bt7)
bt4.insertLeft(bt8)
bt6.insertRight(bt10)
bt6.insertLeft(bt9)
ca = getCommonAncestor(bt7,bt5)
if ca != None:
ca = ca.getValue()
print("The CA between {} and {} is: {}".format(bt7.getValue(),
bt5.getValue(),
ca))
ca = getCommonAncestor(bt7,bt10)
if ca != None:
ca = ca.getValue()
print("The CA between {} and {} is: {}".format(bt7.getValue(),
bt10.getValue(),
ca))
ca = getCommonAncestor(bt7,bt8)
if ca != None:
ca = ca.getValue()
print("The CA between {} and {} is: {}".format(bt7.getValue(),
bt8.getValue(),
ca))
ca = getCommonAncestor(bt5b,bt8)
if ca != None:
ca = ca.getValue()
print("The CA between {} and {} is: {}".format(bt5b.getValue(),
bt8.getValue(),
ca))
The CA between 7 and 5 is: 3
The CA between 7 and 10 is: 2
The CA between 7 and 8 is: 4
The CA between 5b and 8 is: Root
Download the complete source file: BinaryTree4.py
A Binary Search Tree is a binary tree with the following properties:
The left subtree of a node contains only nodes with values lower than that of the node.
The right subtree of a node contains only nodes with values greater than the node’s.
No duplicate nodes are allowed.
Implement:
a function
BST = createBST(inList)that gets a list of integers (or strings) and returns a BinaryTree that is a Binary Search Tree;a search function
searchBST(BST, element)that gets an integer (or string) and checks if it is present in the Binary Search Tree.modify the
inOrderDFS(self)method to return a list of visited nodes using in-order depth first search. Test the method by printing the first 100 elements to show that they are actually sorted (this is a sorting algorithm indeed!);
Test the code with the following intList:
import random
intList = []
for i in range(1000):
inList.append(random.randint(0,10000))
Show/Hide Solution
NOTE: This solution shows you how to plot a graph (makes use of pygraphviz, which is an off-topic for this course, go here for details). You can see a sample output of the plot here BST_test.png
[7]:
class BinarySearchTree:
def __init__(self, value):
self.__data = value
self.__right = None
self.__left = None
self.__parent = None
self.__depth = 0 #new param
# new method
def getDepth(self):
return self.__depth
# new method
def setDepth(self, newdepth):
self.__depth = newdepth
def getValue(self):
return self.__data
def setValue(self, newValue):
self.__data = newValue
def getParent(self):
return self.__parent
def setParent(self, tree):
self.__parent = tree
def getRight(self):
return self.__right
def getLeft(self):
return self.__left
def insertRight(self, tree):
if self.__right == None:
self.__right = tree
tree.setParent(self)
#line modified
tree.setDepth(self.getDepth() + 1)
def insertLeft(self, tree):
if self.__left == None:
self.__left = tree
#line modified
tree.setDepth(self.getDepth() + 1)
tree.setParent(self)
def deleteRight(self):
self.__right = None
def deleteLeft(self):
self.__left = None
def inOrderDFS(self):
ret = []
if self != None:
r = self.getRight()
l = self.getLeft()
if l != None:
ret.extend(l.inOrderDFS())
ret.append(self.getValue())
if r != None:
ret.extend(r.inOrderDFS())
return ret
def createBST(intList):
BST = None
if len(intList) > 0:
BST = BinarySearchTree(intList[0])
for el in intList[1:]:
cur_el = BST
alreadyPresent = False
prev_el = None
while cur_el != None:
prev_el = cur_el
cv = cur_el.getValue()
if cv > el:
cur_el = cur_el.getLeft()
elif cv < el:
cur_el = cur_el.getRight()
else:
# cv == el (el is already present)
# not allowed by rule c, so skip it
alreadyPresent = True
#print("El {} already present".format(el))
break
if not alreadyPresent:
node = BinarySearchTree(el)
node.setParent(prev_el)
if prev_el.getValue() > el:
prev_el.insertLeft(node)
else:
prev_el.insertRight(node)
return BST
def searchBST(BST, element):
if BST == None or element == None:
return False
else:
cur_el = BST
while cur_el != None:
if cur_el.getValue() == element:
return True
else:
if cur_el.getValue()> element:
cur_el = cur_el.getLeft()
else:
cur_el = cur_el.getRight()
return False
def printTree(root):
cur = root
#each element is a node and a depth
#depth is used to format prints (with tabs)
nodes = [(cur,0)]
tabs = ""
lev = 0
while len(nodes) >0:
cur, lev = nodes.pop(-1)
#print("{}{}".format("\t"*lev, cur.getValue()))
if cur.getRight() != None:
print ("{}{} (r)-> {}".format("\t"*lev,
cur.getValue(),
cur.getRight().getValue()))
nodes.append((cur.getRight(), lev+1))
if cur.getLeft() != None:
print ("{}{} (l)-> {}".format("\t"*lev,
cur.getValue(),
cur.getLeft().getValue()))
nodes.append((cur.getLeft(), lev+1))
def plotGraph(tree):
#uses pygraphviz
G=pgv.AGraph(directed=True)
levels = [tree]
while len(levels) > 0:
cur_n = levels.pop()
if cur_n != None:
G.add_node(cur_n.getValue(), color = 'black')
r = cur_n.getRight()
l = cur_n.getLeft()
if l != None:
G.add_node(l.getValue(), color = 'black')
G.add_edge(cur_n.getValue(), l.getValue())
levels.append(l)
if r != None:
G.add_node(r.getValue(), color = 'black')
G.add_edge(cur_n.getValue(), r.getValue())
levels.append(r)
G.layout(prog='dot') # use dot
#In the following, the path of the graph. Change
#it to your liking
G.draw('images/BST_test.png')
if __name__ == "__main__":
import random
#import pygraphviz as pgv
#import time
inList = []
for i in range(1000):
inList.append(random.randint(0,10000))
BST = createBST(inList)
#printTree(BST)
#plotGraph(BST)
for i in range(100):
v = random.randint(0,100)
#s_t = time.time()
ok = searchBST(BST, v)
#e_t = time.time()
okL = v in inList
#e_t2 = time.time()
print("el {} : present? {}".format(v, ok))
#print("Time BST:{:.6f} list:{:.6f}".format(e_t - s_t,
# e_t2 - e_t
# ))
assert(ok == okL)
sorted = BST.inOrderDFS()
print("\nIn order DFS (first 100 elements):")
print(sorted[0:100])
el 87 : present? True
el 24 : present? False
el 22 : present? False
el 67 : present? False
el 76 : present? False
el 10 : present? False
el 58 : present? False
el 71 : present? False
el 90 : present? False
el 16 : present? False
el 96 : present? False
el 52 : present? False
el 36 : present? False
el 39 : present? False
el 90 : present? False
el 82 : present? False
el 48 : present? False
el 94 : present? False
el 25 : present? False
el 33 : present? False
el 61 : present? False
el 0 : present? False
el 90 : present? False
el 46 : present? False
el 31 : present? False
el 38 : present? False
el 25 : present? False
el 4 : present? False
el 62 : present? False
el 100 : present? False
el 34 : present? False
el 92 : present? False
el 14 : present? False
el 13 : present? False
el 69 : present? True
el 65 : present? False
el 8 : present? False
el 58 : present? False
el 26 : present? False
el 48 : present? False
el 4 : present? False
el 63 : present? False
el 2 : present? True
el 76 : present? False
el 51 : present? False
el 76 : present? False
el 13 : present? False
el 18 : present? False
el 24 : present? False
el 18 : present? False
el 80 : present? False
el 14 : present? False
el 27 : present? False
el 76 : present? False
el 40 : present? True
el 74 : present? False
el 3 : present? False
el 9 : present? False
el 91 : present? False
el 82 : present? False
el 85 : present? False
el 50 : present? False
el 36 : present? False
el 100 : present? False
el 44 : present? False
el 27 : present? False
el 40 : present? True
el 55 : present? False
el 46 : present? False
el 31 : present? False
el 4 : present? False
el 23 : present? False
el 17 : present? False
el 55 : present? False
el 63 : present? False
el 69 : present? True
el 21 : present? False
el 74 : present? False
el 13 : present? False
el 52 : present? False
el 1 : present? False
el 0 : present? False
el 57 : present? False
el 63 : present? False
el 59 : present? False
el 32 : present? True
el 85 : present? False
el 37 : present? False
el 100 : present? False
el 62 : present? False
el 19 : present? False
el 90 : present? False
el 59 : present? False
el 60 : present? False
el 80 : present? False
el 97 : present? False
el 65 : present? False
el 31 : present? False
el 62 : present? False
el 86 : present? False
In order DFS (first 100 elements):
[2, 32, 40, 41, 56, 69, 72, 83, 87, 88, 98, 108, 111, 126, 129, 142, 224, 231, 240, 257, 259, 260, 275, 278, 281, 283, 297, 298, 307, 319, 336, 340, 351, 376, 383, 393, 402, 408, 423, 428, 431, 440, 463, 498, 511, 517, 520, 525, 532, 558, 569, 595, 597, 600, 617, 626, 630, 637, 652, 659, 672, 715, 717, 736, 744, 747, 765, 779, 796, 798, 802, 813, 832, 837, 841, 855, 872, 896, 912, 916, 928, 942, 963, 973, 994, 1002, 1013, 1015, 1017, 1035, 1047, 1061, 1069, 1078, 1081, 1088, 1090, 1093, 1094, 1098]
Download the complete source file: BinarySearchTree.py
ADT: Generic Tree
Generic Trees are like binary trees, but each node can have more than 2 children. One possible implementation is that each node (that is a subtree in itself) has a value, a link to its parent and a list of children.
Another implementation is that each node has a value, a link to its parent, a link to its next sibling and a link to its first child:
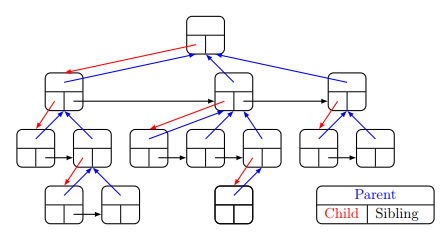
We will be using this latter implementation of the tree.
The Generic Tree ADT seen at lecture follows:
Given the following generic tree:
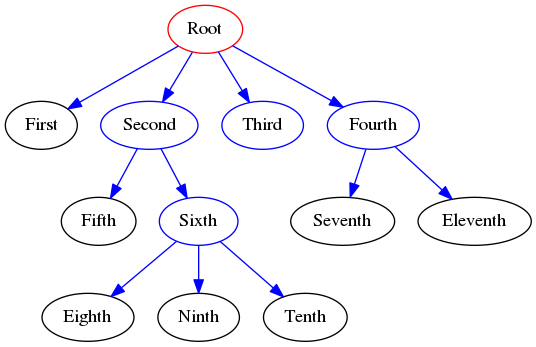
Exercise (implementation)
Implement the
GenericTreeclass representing the ADT seen above and create the tree in the picture above.
Show/Hide Solution
[8]:
class GenericTree:
def __init__(self, value):
self.__data = value
self.__parent = None
self.__child = None
self.__sibling = None
def getValue(self):
return self.__data
def setValue(self,newvalue):
self.__data = newvalue
def getParent(self):
return self.__parent
def setParent(self, parent):
self.__parent = parent
def getLeftmostChild(self):
return self.__child
def getSibling(self):
return self.__sibling
def setSibling(self,sib):
self.__sibling = sib
def insertSibling(self,sib):
if type(sib) != GenericTree:
raise TypeError("parameter sib is not a GenericTree")
else:
nextS = None
if self.__sibling != None:
nextS = self.__sibling
self.__sibling = sib
sib.setParent(self.getParent())
sib.setSibling(nextS)
def insertChild(self,child):
if type(child) != GenericTree:
raise TypeError("parameter child is not a GenericTree")
else:
nextC = None
print("from {} adding child --> {}".format(self.getValue(),
child.getValue()))
if self.__child != None:
nextC = self.__child
child.setParent(self)
child.setSibling(nextC)
self.__child = child
def deleteChild(self):
if self.__child != None:
#moves along the sibling structure of child
self.__child = self.__child.getSibling()
def deleteSibling(self):
if self.__sibling != None:
#moves along the sibling structure of the sibling
self.__sibling = self.__sibling.getSibling()
if __name__ == "__main__":
g = GenericTree("Root")
g1 = GenericTree("First")
g2 = GenericTree("Second")
g3 = GenericTree("Third")
g4 = GenericTree("Fourth")
g5 = GenericTree("Fifth")
g6 = GenericTree("Sixth")
g7 = GenericTree("Seventh")
g8 = GenericTree("Eighth")
g9 = GenericTree("Ninth")
g10 = GenericTree("Tenth")
g11 = GenericTree("Eleventh")
#root
g.insertChild(g4)
g.insertChild(g3)
g.insertChild(g2)
g.insertChild(g1)
#second
g2.insertChild(g6)
g2.insertChild(g5)
#fourth
g4.insertChild(g7)
g7.insertSibling(g11)
#sixth
g6.insertChild(g10)
g6.insertChild(g9)
g6.insertChild(g8)
#let's print some stuff
nodes = [g,g1,g2,g3,g4,g5,g6,g7,g8,g9,g10,g11]
for n in nodes:
print("Node {}:".format(n.getValue()))
par = n.getParent()
if par != None:
par = par.getValue()
print("\t has parent: {}".format(par))
c = n.getLeftmostChild()
children = []
if c != None:
children.append(c.getValue())
nc = c.getSibling()
while nc != None:
children.append(nc.getValue())
nc = nc.getSibling()
print("\t has children: {}".format(",".join(children)))
s = n.getSibling()
sibs = []
if s != None:
sibs.append(s.getValue())
ns = s.getSibling()
while ns != None:
sibs.append(ns.getValue())
ns = ns.getSibling()
print("\t has next siblings: {}".format(",".join(sibs)))
from Root adding child --> Fourth
from Root adding child --> Third
from Root adding child --> Second
from Root adding child --> First
from Second adding child --> Sixth
from Second adding child --> Fifth
from Fourth adding child --> Seventh
from Sixth adding child --> Tenth
from Sixth adding child --> Ninth
from Sixth adding child --> Eighth
Node Root:
has parent: None
has children: First,Second,Third,Fourth
has next siblings:
Node First:
has parent: Root
has children:
has next siblings: Second,Third,Fourth
Node Second:
has parent: Root
has children: Fifth,Sixth
has next siblings: Third,Fourth
Node Third:
has parent: Root
has children:
has next siblings: Fourth
Node Fourth:
has parent: Root
has children: Seventh,Eleventh
has next siblings:
Node Fifth:
has parent: Second
has children:
has next siblings: Sixth
Node Sixth:
has parent: Second
has children: Eighth,Ninth,Tenth
has next siblings:
Node Seventh:
has parent: Fourth
has children:
has next siblings: Eleventh
Node Eighth:
has parent: Sixth
has children:
has next siblings: Ninth,Tenth
Node Ninth:
has parent: Sixth
has children:
has next siblings: Tenth
Node Tenth:
has parent: Sixth
has children:
has next siblings:
Node Eleventh:
has parent: Fourth
has children:
has next siblings:
Note that the sibling list is actually unidirectional therefore “Second” does not any way to know that it is on the same level of “First”.
Download the complete source file: GenericTree.py