Module 2, Practical 2

In this practical we will learn how to test a Python program and how to measure its runtime and memory usage (i.e., compexity in time and space).

Testing

Testing a software product allows to check whether the written code actually yields the expected results. In particular, testing the execution of code is called dynamic testing.

In Python, we can use assert to quickly test that functions we have written behave as they should:

assert(condition)

condition must be True for program execution to continue without errors.

If it is False, an AssertionError exception will be raised.

[1]:

def sumOfTwo(x, y):
    return x + y

# this should return 8
sumOfTwo(3,5)

# check that the function is working properly
assert(sumOfTwo(3,5) == 8)

# what happens here?
assert(sumOfTwo(3,5) == 1)

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
Cell In[1], line 11
      8 assert(sumOfTwo(3,5) == 8)
     10 # what happens here?
---> 11 assert(sumOfTwo(3,5) == 1)

AssertionError:

Always remember that these tests are not exhaustive, they check only specific aspects of the function and a subset of possible inputs.

For example, what happens if the user provides one integer and one string as parameters?

[2]:

sumOfTwo(3, "baduser")

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[2], line 1
----> 1 sumOfTwo(3, "baduser")

Cell In[1], line 2, in sumOfTwo(x, y)
      1 def sumOfTwo(x, y):
----> 2     return x + y

TypeError: unsupported operand type(s) for +: 'int' and 'str'

Unit testing

Unit testing refers to tests that verify the functionality of a code unit, typically a function. Asserts are a quick way to test a piece of code but they don’t provide us with much detail (e.g. how different is the result we obtained from the expected one?). Luckily, Python provides us with a specific module for unit testing: unittest (see here the doc).

unittest is an OOP-based module - you need to subclass the unittest.TestCase class:

[3]:

import unittest

def fibonacci(n):
    lst = []
    for i in range(0, n):
        if(i <= 1):
            lst.append(1)
        else:
            lst.append(lst[i-2] + lst[i-1])
    return(lst)

print("Fibonacci(5):", fibonacci(5))

class FibonacciTest(unittest.TestCase):

    def test_listLength(self):
        self.assertEqual(len(fibonacci(4)), 4)

Fibonacci(5): [1, 1, 2, 3, 5]

The test methods name begins with test_.

unittest offers many types of assertions: assertTrue, assertEqual, assertListEquals and more.

In a command-line environment, the unit test woud be launched by typing: python3 -m unittest file_test

So to run these code chunks, save the code in a test.py file and run it from the terminal

Example

Try yourself to complete the FibonacciTest class by adding the following asserts:

check that the last (highest) number is correct
check that a negative n provided as input does not break the function
check that a floating point n as input does not break the function

Show/Hide solution

[4]:

import unittest

def fibonacci(n):
    lst = []
    for i in range(0, n):
        if(i <= 1):
            lst.append(1)
        else:
            lst.append(lst[i-2] + lst[i-1])
    return(lst)

print("Fibonacci(5):", fibonacci(5))

class FibonacciTest(unittest.TestCase):

    def test_listLength(self):
        self.assertEqual(len(fibonacci(4)), 4) # fibonacci(4)) returns 4 numbers

    def test_checkLast(self):
        self.assertEqual(max(fibonacci(5)), 5) # last number of fibonacci(5)) is 5

    def test_checkNegative(self):
        self.assertIsNotNone(fibonacci(-10)) # fibonacci(-10) returns something

    def test_checkFloatingPoint(self):
        self.assertIsNotNone(fibonacci(4.5)) # what happens here?

Fibonacci(5): [1, 1, 2, 3, 5]

The checkFloatingPoint test fails. Let’s fix the fibonacci function to solve the issue and run the unit tests again!

What if we decide to not accept a floating point input? We can raise a TypeError exception and modify the unit test accordingly.

For a preliminary guide to Python exceptions, please refer to the official Python tutorial: https://docs.python.org/3/tutorial/errors.html

[5]:

import unittest

def fibonacci(n):
    if isinstance(n, int):
        lst = []
        for i in range(0, n):
            if(i <= 1):
                lst.append(1)
            else:
                lst.append(lst[i-2] + lst[i-1])
        return(lst)
    else:
        raise(TypeError) # we raise an exception!

print("Fibonacci(5):", fibonacci(5))

class FibonacciTest(unittest.TestCase):

    def test_listLength(self):
        self.assertEqual(len(fibonacci(4)), 4) # fibonacci(4)) returns 4 numbers

    def test_checkLast(self):
        self.assertEqual(max(fibonacci(5)), 5) # last number of fibonacci(5)) is 5

    def test_checkNegative(self):
        self.assertIsNotNone(fibonacci(-10)) # fibonacci(-10) returns something

    def test_checkFloatingPoint(self):
        with self.assertRaises(TypeError): # fibonacci(4.5) has to raise an exception
            fibonacci(4.5)

Fibonacci(5): [1, 1, 2, 3, 5]

Exercise

Modify the FibonacciTest class to:

raise a ValueError exception if the provided n is negative
check that a big n (>>100, for example 100,000) does not raise a MemoryError exception

Show/Hide solution

[6]:

import unittest

def fibonacci(n):
    if isinstance(n, int):
        if n > 0:
            lst = []
            for i in range(0, n):
                if(i <= 1):
                    lst.append(1)
                else:
                    lst.append(lst[i-2] + lst[i-1])
            return(lst)
        else:
            raise(ValueError) # we raise an exception!
    else:
        raise(TypeError) # we raise another exception!

print("Fibonacci(5):", fibonacci(5))

class FibonacciTest(unittest.TestCase):

    def test_listLength(self):
        self.assertEqual(len(fibonacci(4)), 4) # fibonacci(4)) returns 4 numbers

    def test_checkLast(self):
        self.assertEqual(max(fibonacci(5)), 5) # last number of fibonacci(5)) is 5

    def test_checkNegative(self):
        with self.assertRaises(ValueError):
            fibonacci(-10) # fibonacci(-10) has to raise an exception this time...

    def test_checkFloatingPoint(self):
        with self.assertRaises(TypeError): # fibonacci(4.5) has to raise an exception
            fibonacci(4.5)

    def test_checkBig(self):
        self.assertIsNotNone(fibonacci(100000)) # test fibonacci(100000) for memory issues

Fibonacci(5): [1, 1, 2, 3, 5]

Measuring time

Another aspect of testing is to probe the time and memory required by your algorithms to be executed under different inputs and parameters.

Python provides the timeit package to measure the execution time of small snippets of code.

Execution of the snippet is repeated multiple times (number parameter) to allow obtaining an estimate also for the quickest snippets :

[ ]:

import pandas as pd
import matplotlib.pyplot as plt
import timeit

def fibonacci(n):
    if isinstance(n, int):
        if n > 0:
            lst = []
            for i in range(0, n):
                if(i <= 1):
                    lst.append(1)
                else:
                    lst.append(lst[i-2] + lst[i-1])
            return(lst)
        else:
            raise(ValueError)
    else:
        raise(TypeError)

# setup ensures that timeit can access specific functions from your local environment
timeit.timeit('fibonacci(5)', number=10000, setup="from __main__ import fibonacci")

times = []
times.append(timeit.timeit('fibonacci(5)', number=10000, setup="from __main__ import fibonacci"))
times.append(timeit.timeit('fibonacci(10)', number=10000, setup="from __main__ import fibonacci"))
times.append(timeit.timeit('fibonacci(15)', number=10000, setup="from __main__ import fibonacci"))

timeSeries = pd.Series(times)
timeSeries.plot()
# to change x labels...
plt.xticks([0, 1, 2], ['fibonacci(5)', 'fibonacci(10)', 'fibonacci(15)'])
plt.show()
plt.close()

Exercise

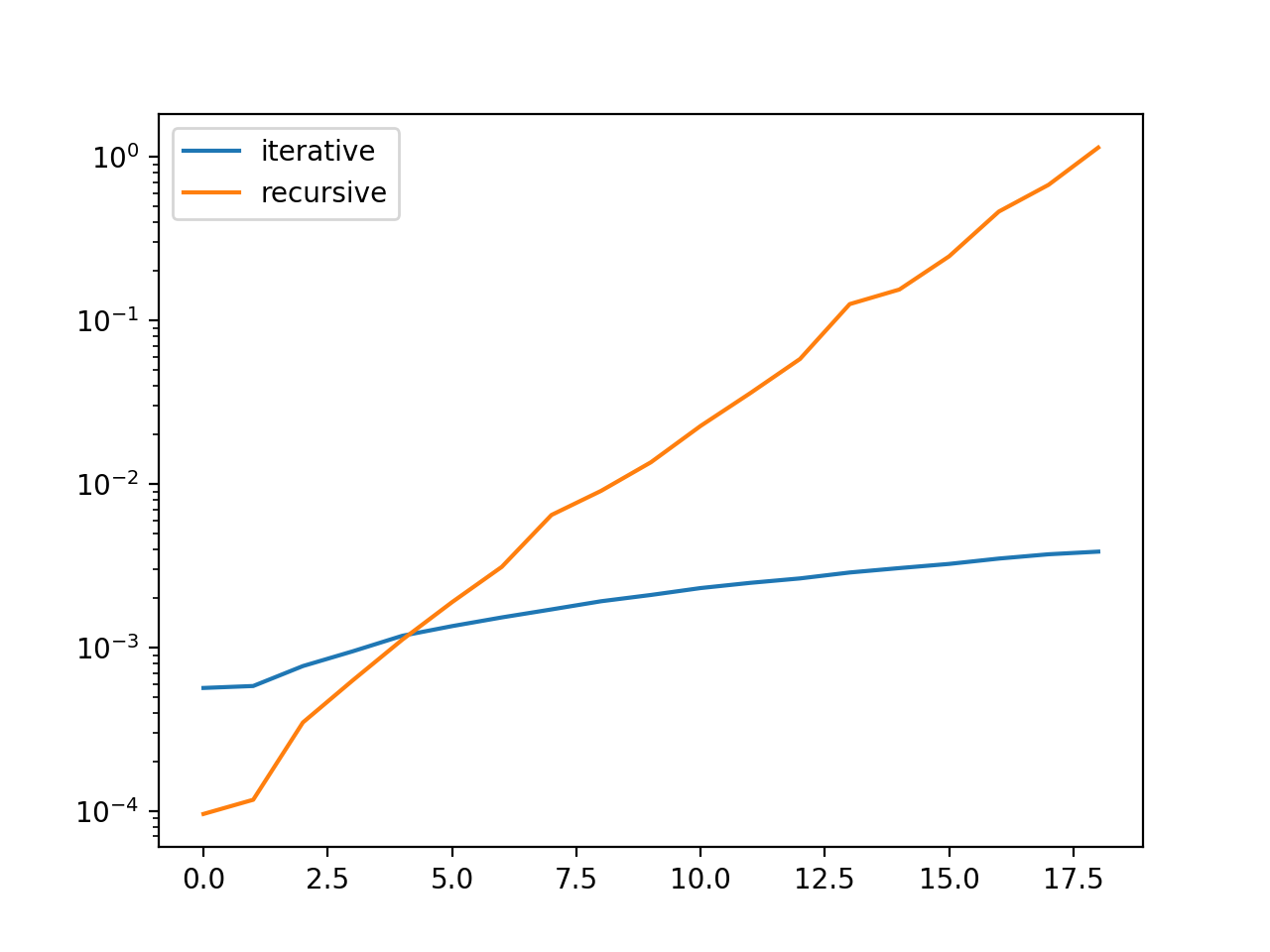
Write the recursiveFibonacci function that computes the n-th Fibonacci number recursively.

Test the execution times of the two fibonacci functions with n ranging from 1 to 20 and plot the two distributions

Show/Hide solution

[ ]:

import pandas as pd
import matplotlib.pyplot as plt
import timeit

def fibonacci(n):
    if isinstance(n, int):
        if n > 0:
            lst = []
            for i in range(0, n):
                if(i <= 1):
                    lst.append(1)
                else:
                    lst.append(lst[i-2] + lst[i-1])
            return(lst)
        else:
            raise(ValueError)
    else:
        raise(TypeError)

def recursiveFibonacci(n):
    if n == 1:
        return 0
    elif n == 2:
        return 1
    else:
        return recursiveFibonacci(n-1) + recursiveFibonacci(n-2)

timesIterative = []
for n in range(1, 20):
    timesIterative.append(timeit.timeit('fibonacci(+' + str(n) + ')', number=1000, setup="from __main__ import fibonacci"))

timesRecursive = []
for n in range(1, 20):
    timesRecursive.append(timeit.timeit('recursiveFibonacci(+' + str(n) + ')', number=1000, setup="from __main__ import recursiveFibonacci"))

timesDict = {'iterative': timesIterative, 'recursive': timesRecursive}
timesDf = pd.DataFrame(timesDict)
timesDf.plot(logy=True) # plot times in logarithmic scale to highlight differences
plt.show()
plt.close()

Measuring memory

Memory used by an object, function or full Python scripts can be measured by different means.

The sys.getsizeof method is one of them:

[3]:

import sys

l1 = [1]*200
l2 = [2]*400

print(sys.getsizeof(l1))
print(sys.getsizeof(l2))

1656
3256

However, measuring the memory footprint of a whole function (rather than single objects), would be much more useful.

We can achieve that, for instance, with the memory-profiler package.

You can install it with pip: pip install -U memory_profiler

[ ]:

# Save this file as memProfSample.py

from memory_profiler import profile

@profile
def allocatingFunction():
    a = [1] * (10 ** 6)
    b = [2] * (2 * 10 ** 7)
    del b
    return a

if __name__ == '__main__':
    allocatingFunction()

[ ]:

Filename: memProfSample.py

Line #    Mem usage    Increment  Occurences   Line Contents
============================================================
     5     39.9 MiB     39.9 MiB           1   @profile
     6                                         def allocatingFunction():
     7     47.5 MiB      7.6 MiB           1       a = [1] * (10 ** 6)
     8    200.1 MiB    152.6 MiB           1       b = [2] * (2 * 10 ** 7)
     9     47.5 MiB   -152.6 MiB           1       del b
    10     47.5 MiB      0.0 MiB           1       return a

Exercise

Test the functionalities introduced in this practical to analyze some of the programs developed during the past lessons.