Module 2, Practical 3¶

Complexity¶

The complexity of an algorithm can be defined as a function mapping the size of the input to the time required to get the result. This is also called the cost function.

There exist several asymptotic (time-measuring) notations. Informally they are:

• Big Omega (best case)

• Big Theta (average case)

• Big O (worst case)

The upper-bound complexity O (the big-Oh) is generally the most interesting to analyze. In this practical we will work with this notation considering several Python code samples.

Big O is a formal notation that describes the behaviour of a function when the argument tends towards the maximum input. Big O takes the upper bound, that is, it considers the worst-case results, the worst execution of the algorithm.

Instead of saying the input is 10 billion, or infinite, we say the input is n size. The exact size of the input doesn’t matter, we only care of how our algorithm performs with the worst input. This approach allows to still work with Big O even if we do not know the exact size of the input during the code execution.

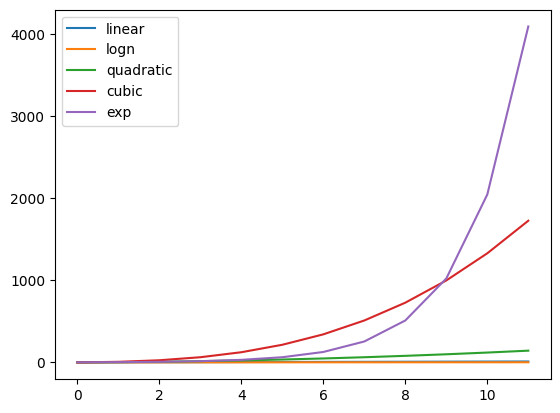
Big O is easy to read once we learn the different order of growth:

[5]:

import math
import pandas as pd
import matplotlib.pyplot as plt

inputList = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]

linear  = [n for n in inputList]
logn  = [math.log(n) for n in inputList]
quadratic  = [n*n for n in inputList]
cubic = [n*n*n for n in inputList]
exponential = [2**n for n in inputList]

functDict = {'linear': linear, "logn": logn, "quadratic": quadratic, "cubic": cubic, "exp": exponential}
functDf = pd.DataFrame(functDict)
functDf.plot()
plt.show()
plt.close()


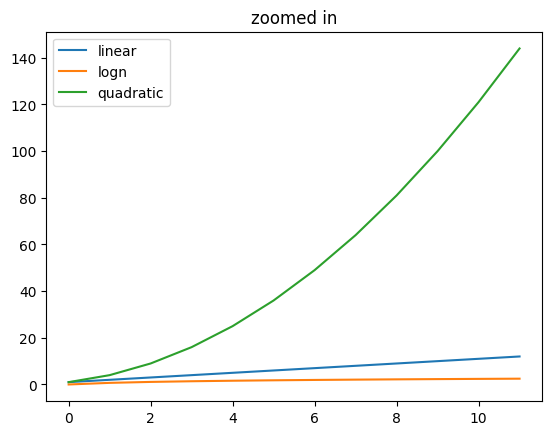
functDf[["linear", "logn", "quadratic"]].plot()
plt.title("zoomed in")
plt.show()

[2]:

def printList(inputList):
    for item in inputList:
        print(item)

printList([4, 5, 6, 8])

print("---------------------")

def printListBothDirections(inputList):
    print("Forward:")
    for item in inputList:
        print(item)
    print("Reverse:")
    for item in inputList[::-1]:
        print(item)

printListBothDirections([4, 5, 6, 8])

4
5
6
8
---------------------
Forward:
4
5
6
8
Reverse:
8
6
5
4

[3]:

def computeHighest(l1, l2):
    for i1 in l1:
        for i2 in l2:
            if i1 > i2:
                print("Value {} in l1 greater than value {} in l2".format(i1, i2))

computeHighest([4, 5, 6, 8], [12,1,42,11])

Value 4 in l1 greater than value 1 in l2
Value 5 in l1 greater than value 1 in l2
Value 6 in l1 greater than value 1 in l2
Value 8 in l1 greater than value 1 in l2

[4]:

def myFunction(items):

    for i in reversed(range(1, 5)):
        print ("{} seconds left".format(i))
    print("boom!\n--------------")

    itemsString = ""
    for item in items:
        itemsString += ">{}".format(item)
    print(itemsString[1:])

    print("--------------")

    pairwiseProducts = []
    for item1 in items:
        for item2 in items:
            if (item1 == item2):
                print("I'm in the diagonal {} {}".format(item1, item2))
            pairwiseProducts.append(item1*item2)

myFunction([4, 5, 6, 8, 12, 14])

4 seconds left
3 seconds left
2 seconds left
1 seconds left
boom!
--------------
4>5>6>8>12>14
--------------
I'm in the diagonal 4 4
I'm in the diagonal 5 5
I'm in the diagonal 6 6
I'm in the diagonal 8 8
I'm in the diagonal 12 12
I'm in the diagonal 14 14

[5]:

def listHalver(inputList):
    sliced = inputList
    while len(sliced) >= 2:
        sliced = sliced[:int(len(sliced)/2)]
        print(sliced)

listHalver([1, 2, 3, 4, 5, 6, 7, 8, 9])
print("------------")

def halverStepper(maxListLength):
    for step in reversed(range(1, maxListLength)):
        listHalver(list(range(1, step)))

halverStepper(12)

[1, 2, 3, 4]
[1, 2]
[1]
------------
[1, 2, 3, 4, 5]
[1, 2]
[1]
[1, 2, 3, 4]
[1, 2]
[1]
[1, 2, 3, 4]
[1, 2]
[1]
[1, 2, 3]
[1]
[1, 2, 3]
[1]
[1, 2]
[1]
[1, 2]
[1]
[1]
[1]

Exercises¶

1. Let M be a square matrix - a list containing n lists, each of them of size n. Return the computational complexity of function fun() with respect to n:

[ ]:

def fun(M):
    for row in M:
        for element in row:
            print(sum([x for x in row if x != element]))

2. Given a list L of n elements, please compute the asymptotic computational complexity of the following function, explaining your reasoning.

[ ]:

def my_fun(L):
    n = len(L)
    tmp = []
    for i in range(int(n)):
        tmp.insert(0,L[i]-L[int(n/3)])
    return sum(tmp)

3. Given a sorted list alist of n elements, please compute the asymptotic computational complexity of the following function implementing binary search, explaining your reasoning.

[ ]:

def binarySearch(alist, item):
    first = 0
    last = len(alist)-1
    found = False

    while first <= last and not found:
        midpoint = (first + last)//2
        if alist[midpoint] == item:
            found = True
        else:
            if item < alist[midpoint]:
            last = midpoint-1
            else:
                first = midpoint+1

    return found

4. Please compute the asymptotic computational complexity of the following code, that computes the Fibonacci sequence according to the following formula:

• If n is even, then k = n/2 and F(n) = [2*F(k-1) + F(k)]*F(k)

• If n is odd, then k = (n + 1)/2 and F(n) = F(k)*F(k) + F(k-1)*F(k-1).

[ ]:

# Create an array of length n for memoization (we will see later what memoization is...)
n = 10
f = [0] * n

# Returns n'th fibonacci number using table f[]
def fib(n) :
    # Base cases
    if (n == 0) :
        return 0
    if (n == 1 or n == 2) :
        f[n] = 1
        return (f[n])

    # If fib(n) is already computed (thanks to memoization)
    if (f[n]):
        return f[n]

    # Applying above formula [Note value n&1 is 1
    # if n is odd, else 0.
    if((n & 1)):
        # (n & 1) is 1 when n is odd, 0 otherwise
        k = (n + 1) // 2
        f[n] = (fib(k) * fib(k) + fib(k-1) * fib(k-1))
    else :
        k = n // 2
        f[n] = (2*fib(k-1) + fib(k))*fib(k)

    return f[n]


# main code
for i in range(n):
    print(fib(i), end=' ') # avoids to add a new line at each iteration
print('') # to go to new line at the end

5. Please compute the asymptotic computational complexity of the function subsets, that computes all the subsets of a set of elements.

Subsets of {a,b}: {(), ('b',), ('a',), ('b', 'a')}
Subsets of {a,b,c}: {(), ('b',), ('a',), ('c',), ('b', 'a'), ('b', 'c'), ('a', 'c'), ('b', 'a', 'c')}

[ ]:

from itertools import chain, combinations

def subsets(elementSet):
    return set(chain.from_iterable(combinations(elementSet, r) for r in range(len(elementSet)+1)))

print('Subsets of {a,b}:', subsets({'a','b'}))
print('Subsets of {a,b,c}:', subsets({'a','b','c'}))