Module 2, Practical 10¶

In this practical we will experiment with programming paradigms.

In particular, we will briefly introduce the dynamic programming technique.

Dynamic programming¶

Dynamic programming is a strategy to optimize recursive algorithms.
Every time we find an algorithm solving a bigger problem by repetitive recursive calls on smaller subproblems, we can optimize it by using dynamic programming.
The key idea is simply to store in a table the solution of the subproblems and obtain the result of these subproblems by performing a table lookup.

Two approaches exist:

Top-down: solve the problem by breaking it down in smaller subproblems. If the subproblem has already been solved, then the answer has already been saved somewhere. If it has not already been solved, compute a solution and store it. This method is called memoization;
Bottom-up: solve the problem by starting from the most trivial subproblems, going up until the complete problem has been solved. Smaller subproblems are guaranteed to be solved before bigger ones. This method is called dynamic programming.

Consider the classic example of the computation of Fibonacci numbers:

\[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...\]

which can be computed by the following recursive formula:

\[\begin{split}F(n)=\left\{ \begin{array}{ll} n & if\ n == 0\ or\ n\ == 1\\ F(n-1)+ F(n-2) & if\ n > 1 \end{array} \right.\end{split}\]

This problem can be solved with the following recursive code:

[1]:

import time

def fib(n):
    if n <= 1:
        return n
    else:
        return fib(n - 1) + fib(n - 2)


for i in range(20):
    print("Fib({})= {}".format(i, fib(i)))


for i in range(35,40):
    start_t = time.time()
    print("\nFib({})= {}".format(i, fib(i)))
    end_t = time.time()
    print("It took {:.2f}s".format(end_t-start_t))

Fib(0)= 0
Fib(1)= 1
Fib(2)= 1
Fib(3)= 2
Fib(4)= 3
Fib(5)= 5
Fib(6)= 8
Fib(7)= 13
Fib(8)= 21
Fib(9)= 34
Fib(10)= 55
Fib(11)= 89
Fib(12)= 144
Fib(13)= 233
Fib(14)= 377
Fib(15)= 610
Fib(16)= 987
Fib(17)= 1597
Fib(18)= 2584
Fib(19)= 4181

Fib(35)= 9227465
It took 5.47s

Fib(36)= 14930352
It took 8.76s

Fib(37)= 24157817
It took 12.93s

Fib(38)= 39088169
It took 21.43s

Fib(39)= 63245986
It took 33.32s

Although simple to code, the recursive solution performs some steps multiple times, as shown by the following recursion tree (for example f(3) is computed 5 times):

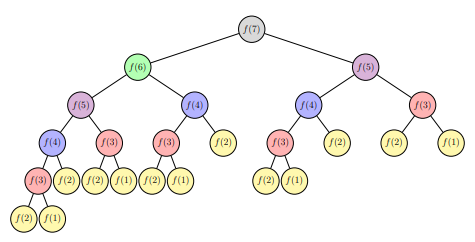
We can use dynamic programming to avoid computing over and over again the same values:

[2]:

import time

def fib_dp(n):
    fib = [0]* (n+1)
    if n > 1:
        fib[1] = 1

    for i in range(2, n + 1):
        fib[i] = fib[i - 2] + fib[i - 1]

    return fib[n]

for i in range(20):
    print("Fib({})= {}".format(i, fib_dp(i)))


for i in range(35,38):
    start_t = time.time()
    print("\nFib({})= {}".format(i, fib_dp(i)))
    end_t = time.time()
    print("It took {:.2f}s".format(end_t - start_t))

#we can even do:
for i in range(1000,1003):
    start_t = time.time()
    print("\nFib({})= {}".format(i, fib_dp(i)))
    end_t = time.time()
    print("It took {:.2f}s".format(end_t - start_t))

Fib(0)= 0
Fib(1)= 0
Fib(2)= 1
Fib(3)= 2
Fib(4)= 3
Fib(5)= 5
Fib(6)= 8
Fib(7)= 13
Fib(8)= 21
Fib(9)= 34
Fib(10)= 55
Fib(11)= 89
Fib(12)= 144
Fib(13)= 233
Fib(14)= 377
Fib(15)= 610
Fib(16)= 987
Fib(17)= 1597
Fib(18)= 2584
Fib(19)= 4181

Fib(35)= 9227465
It took 0.00s

Fib(36)= 14930352
It took 0.00s

Fib(37)= 24157817
It took 0.00s

Fib(1000)= 43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875
It took 0.00s

Fib(1001)= 70330367711422815821835254877183549770181269836358732742604905087154537118196933579742249494562611733487750449241765991088186363265450223647106012053374121273867339111198139373125598767690091902245245323403501
It took 0.00s

Fib(1002)= 113796925398360272257523782552224175572745930353730513145086634176691092536145985470146129334641866902783673042322088625863396052888690096969577173696370562180400527049497109023054114771394568040040412172632376
It took 0.00s

In the latter case we accumulated partial results in a list and re-used them when needed. Consider the following code:

[3]:

import time

def fib_dp(n):
    fib = [0]* (n+1)
    if n > 1:
        fib[1] = 1

    for i in range(2,n + 1):
        fib[i] = fib[i - 2] + fib[i - 1]

    return fib[n]


start_t = time.time()
for i in range(1,15000):
    r = fib_dp(i)
end_t = time.time()
print("It took {:.2f}s".format(end_t-start_t))

It took 46.38s

In this case we repeated the computations several times anyway and had to recompute the solution all the time, which is a little bit of a waste of time. If we are not concerned about using more space we could modify the code in such a way to update a list and return the whole list, ready for a next iteration:

[4]:

import time

def fib_dpV2(n,fibList):
    if n < len(fibList):
        return fibList[n]
    else:
        if n == 0:
            fibList.append(0)
            return 0
        if n == 1:
            fibList.extend([0,1])
            return 1
        L = n - len(fibList)
        for i in range(L):
            # compute all the fibonacci values required to reach fib(n) and store them in the list...
            fibList.append(fibList[-2] + fibList[-1])
        return fibList[-1]


start_t = time.time()
myFibL = []
for i in range(1,15001):
    r = fib_dpV2(i, myFibL)
end_t = time.time()
print("Fibonacci(15000) : {}".format(myFibL[-1]))
print("It took {:.2f}s".format(end_t-start_t))
print("Fibonacci 0..20: {}".format(myFibL[0:20]))

Fibonacci(15000) : 180356212817232358527136269558393274270479577287959770214783776455882580176808282935116449287253001675278567205597341664270703993136851989859494809191272208168671602010135312495296553662790352582033423080689757992520655785610316941531173588408998619812807392167094455165363355259485592278979388870298110870050912172411703995878726547708126588747557108886477742159519675726841476567233617069303168933729769224839193682942110633367322841686836744207977400786184404283243942571683714924012584054120950619420879245008334171878098209414559267738476048405512373264705915648256421029922854826089454770481653365776765021018110912210918296748113016817314353185049893148191072970004722127877580853512230597663125482412037507790122452840808247238862266940374952733301348535189028427982115508256085629078838285854519748549211253115363900979738960948772589014559911367102564396479380119671836661458473444680552841046388920629103926658110037230386547506816712866616340383491227279709660200771238944743897531289959511150305531873160607872566720751381188951153762201432960669039121243742888978686571778654570582578356003787537920689451735958244288072349086881269456351988300299442324421142440230312335818179554507414851349917896307630882698214864014344956780348499120670367075038565963319741348415248138037342603113034434198363994519415494026021710622105031596662576344941382709460665227123428132640271682951472209368453748754510035741638613590279538796566181871895713339174456728394471357415996934436202565485732749272347348991793493320243181956465786389970599533658454386144770652584880176519203467064567384636418219255416950945755037995377546451320680325530900980211314010182766809827492194845387482751225482662997765661866262382112219008183345652570682633899549560294736097218086788785294700336993482784319083980440026327099112563241621005721911339313568395785607613027063516725870186041444932874242502339316433484868302535616417673857358757000197098734066555060275659441540730179880840068680711039092402469979537402038522869532858210224421954879125281803617171486680299882175622463954938841161683824017764172124148438928242788323301450705633955505182591808014745581257657569980476219657313856171171041106956687416108450931365450698373196534957320986723454445945232416845732305494189207716358085853199984634824143123729540264742981573020172237026058046740201545250287662018382140146169998065636288937211877886621661690578651489040221004254744005525689460483194423394923570500857169107685204978377809144999120496376447004389621794981767672901579794816635242858841182877011991980777649470507584848234893126914722042071134658473351945026030226538176505680011883028482299815999170838410236573499975247752075137709072936793331605370102620992579010729955042839150039536988476316814658001111401786786920802580057225089821741914525126541381743907218686111921778056456742847181643346546263899570276608898254139702386798819800561168979805761661085945938400171610214159378775050985949240013649311708619468421748433514761538254173535727874452760668054213182096783214642043675647412439936425441952983174011449159555969819986536279264099966926245798558475510001
It took 0.02s
Fibonacci 0..20: [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]

Excercise¶

Catalan numbers (info here) are defined by the following recurrence equation:

\[\begin{split}C(n)=\left\{ \begin{array}{ll} 1 & if\ n <=1 \\ \sum_{i=0}^{n-1} C(i) C(n-1 -i)& if\ n > 1 \end{array} \right.\end{split}\]

the first few values are reported below:

\(1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786,\) \(208012, 742900, 2674440, 9694845, 35357670, 129644790,\) \(477638700, 1767263190, 6564120420, 24466267020, 91482563640, ...\)

Write a recursive function recCatalan(n) to compute the n-th catalan number;
Write a dynamic programming function dpCatalan(n) to compute the n-th catalan number.

Test your code with:

catN = []
for i in range(0,15):
    catN.append(recCatalan(i))

print("First 15 catalan numbers:")
print(catN)

Finally, check how long it takes to compute the 20th catalan number with the recursive algorithm and with the dynamic programming one.

Show/Hide Solution